Research Statement

My long-term goal is to develop a dependable decision-making strategy to tackle data uncertainty, which is a common challenge in various real-life applications. My research proposed methodologies to study different decision-making problems with offline, noisy, small-sample, or high-dimensional data. On the one hand, we focus on developing computationally efficient methodologies through the lens of modern optimization techniques. On the other hand, we provide strong performance guarantees of the proposed modeling leveraging tools from statistics. More specifically, my research focuses on:

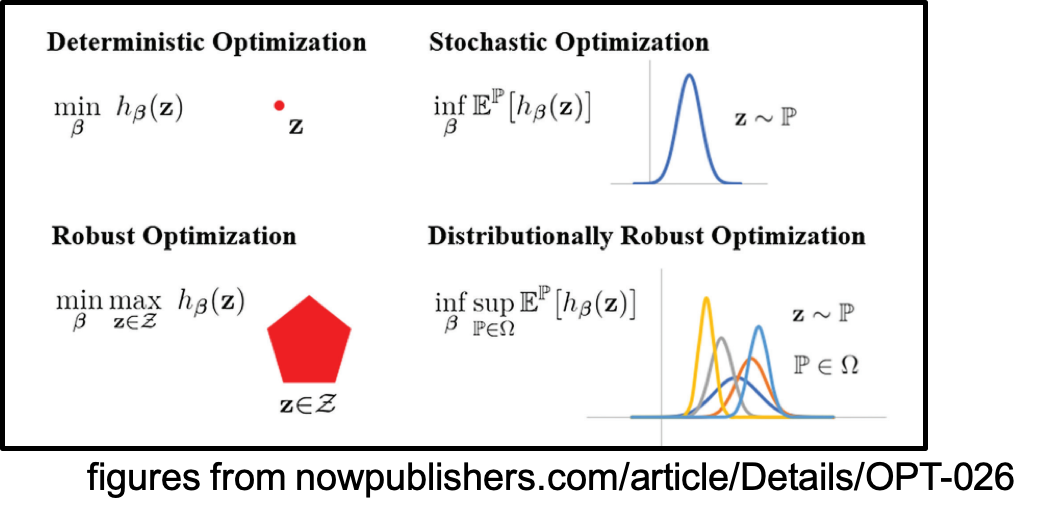
• Distributionally Robust Optimization

• Efficient Statistical Hypothesis Testing

• Reliable Multi-Hop Network Communication

Distributionally Robust Optimization

Distributionally robust optimization (DRO) presents a promising approach to data-driven optimization by finding a minimax robust optimal decision that minimizes the expected loss under the most adverse distribution within a given set of relevant distributions. My research has advanced the theory, algorithms, and applications in this area.

• From a theoretical perspective, I developed a tractable strong dual reformulation for DRO utilizing the entropic-regularized Wasserstein distance, known as Sinkhorn DRO. This model improves the generalization and computational performance compared with the classical Wasserstein DRO model.

• Algorithm-wise, my work introduced a first-order method that efficiently identifies near-optimal solutions with low computational and storage costs. It demonstrates that Sinkhorn DRO can generally be solved with a complexity comparable to that of non-robust empirical risk minimization. As a byproduct of this analysis, we also provide sample complexity for a more general class of problems, including bilevel program and stochastic program whose unbiased gradient oracles are unavailable to query.

• Additionally, I have explored and demonstrated the advantages of DRO across various application domains, including reinforcement learning, hypothesis testing, healthcare, wireless communication, and more. These applications highlight the versatility and effectiveness of the DRO framework in addressing diverse real-world challenges.

1. Multi-level Monte-Carlo Gradient Methods for Stochastic Optimization with Biased Oracles
   Yifan Hu, Jie Wang, Xin Chen, Niao He.

2. Regularization for Adversarial Robust Learning [Slides]
   Jie Wang, Rui Gao, Yao Xie. (Winner of the 18th INFORMS DMDA Workshop Best Paper Competition Award, 2 out of 57)

3. Reliable Off-policy Evaluation for Reinforcement Learning
   Jie Wang, Rui Gao, Hongyuan Zha. Operations Research

4. Sinkhorn Distributionally Robust Optimization [Poster with LaTeX Source File] [Experiment Code]
   Jie Wang, Rui Gao, Yao Xie. Major Revision at Operations Research
   (Winner of 2022 INFORMS Best Poster Award!)

5. Distributionally Robust Degree Optimization for BATS Codes
   Hoover H. F. Yin, Jie Wang, Sherman S. M. Chow. 2024 IEEE International Symposium on Information Theory

6. Non-Convex Robust Hypothesis Testing using Sinkhorn Uncertainty Sets
   Jie Wang, Rui Gao, Yao Xie. 2024 IEEE International Symposium on Information Theory

7. Conditional Stochastic Bilevel Optimization
   Yifan Hu, Jie Wang, Yao Xie, Andreas Krause, Daniel Kuhn. NeurIPS 2023 (Journal version to be submitted to Operations Research)

8. Reliable Adaptive Recoding for Batched Network Coding with Burst-Noise Channels
   Jie Wang, Talha Bozkus, Yao Xie, Urbashi Mitra. Asilomar 2023

9. Improving Sepsis Prediction Model Generalization With Optimal Transport
   Jie Wang, Ronald Moore, Rishikesan Kamaleswaran, Yao Xie. 2022 Machine Learning for Health (ML4H)

10. A Data-Driven Approach to Robust Hypothesis Testing Using Sinkhorn Uncertainty Sets
    Jie Wang, Yao Xie. 2022 IEEE International Symposium on Information Theory (ISIT)

11. Small-Sample Inferred Adaptive Recoding for Batched Network Coding
    Jie Wang, Zhiyuan Jia, Hoover H. F. Yin, Shenghao Yang. 2021 IEEE International Symposium on Information Theory (ISIT)

12. Reliable Offline Pricing in eCommerce Decision-Making: A Distributionally Robust Viewpoint
    Jie Wang. Finalist presentation for the 18th INFORMS DMDA Workshop Data Challenge Competition, 2024

Efficient Statistical Hypothesis Testing

Hypothesis testing has long been a challenge in statistics, involving the decision to accept or reject a null hypothesis based on collected observations. However, classical methods often fall short in addressing the challenges posed by the era of Big Data. In my research, I have developed modern hypothesis testing approaches to tackle these difficulties.

A key focus of my work has been developing efficient hypothesis testing frameworks for high-dimensional data. Traditional methods often suffer significant performance degradation as data dimensionality increases. To address this issue, we utilize nonlinear dimensionality reduction to project data distributions onto low-dimensional spaces with maximum separability before conducting hypothesis tests.

Another area of my research bridges hypothesis testing with deep learning, providing a statistical foundation for reliable machine learning. Our goal is to create systematic tools that offer statistical performance guarantees for hypothesis testing using neural networks. This advancement aims to make modern classification algorithms more dependable and trustworthy, particularly in scientific discovery.

Additionally, I have explored the synergy between hypothesis testing and recent advances in optimization to develop efficient testing methodologies for various scenarios. For example, I employ distributionally robust optimization to create a non-parametric test, assuming that data distributions under each hypothesis belong to “uncertainty sets” constructed using the Sinkhorn discrepancy. Furthermore, I have investigated variable selection for hypothesis testing, aiming to identify a small subset of variables that best distinguish samples from different groups. Due to the inherent sparsity, this problem is often formulated as a challenging NP-hard mixed-integer programming task. Both exact and approximation algorithms are provided to address the computational challenges,

Below I highlight manuscripts related to this topic:

1. Statistical and Computational Guarantees of Kernel Max-Sliced Wasserstein Distances
   Jie Wang, March Boedihardjo, Yao Xie. (Finalist of the INFORMS 2024 Data Mining Best Paper Award Competition)

2. Variable Selection for Kernel Two-Sample Tests
   Jie Wang, Santanu Dey, Yao Xie. (Selected for Poster Presentation at Mixed Integer Programming (MIP) Workshop 2023, to be submitted to Operations Research)
   

3. A Manifold Two-Sample Test Study: Integral Probability Metric with Neural Networks
   Jie Wang, Minshuo Chen, Tuo Zhao, Wenjing Liao, Yao Xie. Information and Inference: A Journal of the IMA

4. Non-Convex Robust Hypothesis Testing using Sinkhorn Uncertainty Sets
   Jie Wang, Rui Gao, Yao Xie. 2024 IEEE International Symposium on Information Theory

5. A Data-Driven Approach to Robust Hypothesis Testing Using Sinkhorn Uncertainty Sets
   Jie Wang, Yao Xie. 2022 IEEE International Symposium on Information Theory (ISIT)

6. Two-sample Test with Kernel Projected Wasserstein Distance
   Jie Wang, Rui Gao, Yao Xie. 2022 Artificial Intelligence and Statistics (AISTATS) (Oral Presentation! Rate: 44/1685=0.026)

7. Two-sample Test using Projected Wasserstein Distance
   Jie Wang, Rui Gao, Yao Xie. 2021 IEEE International Symposium on Information Theory (ISIT)

Reliable Multi-Hop Network Communication

Over the past decade, wireless network communication products such as WiFi and cellular networks have become widely accessible across the globe. However, a common challenge in the industry, known as the “curse of multihop,” involves a significant decrease in network throughput as the number of transmission hops increases. To address this issue, a recently developed technique called batched network coding offers a computationally efficient solution. My research has focused on two key aspects of this technique.

• First, I conducted theoretical analyses to determine the scaling rate of batched network coding concerning hop length, demonstrating its advantages over traditional methods like decode-and-forward.

• Second, I developed an enhanced batched network coding methodology that incorporates considerations for the uncertainty in channel status, further optimizing network performance.

Below I highlight manuscripts related to this topic:

1. On Achievable Rates of Line Networks with Generalized Batched Network Coding
   Jie Wang, Shenghao Yang, Yanyan Dong, Yiheng Zhang. IEEE Journal on Selected Areas in Communications

2. Throughput and Latency Analysis for Line Networks with Outage Links
   Yanyan Dong, Shenghao Yang, Jie Wang, Fan Cheng. IEEE Journal on Selected Areas in Information Theory (Conference version accepted by 2024 IEEE International Symposium on Information Theory)

3. Sparse Degree Optimization for BATS Codes
   Hoover H. F. Yin, Jie Wang. 2024 IEEE Information Theory Workshop

4. Distributionally Robust Degree Optimization for BATS Codes
   Hoover H. F. Yin, Jie Wang, Sherman S. M. Chow. 2024 IEEE International Symposium on Information Theory

5. Reliable Adaptive Recoding for Batched Network Coding with Burst-Noise Channels
   Jie Wang, Talha Bozkus, Yao Xie, Urbashi Mitra. Asilomar 2023

6. Small-Sample Inferred Adaptive Recoding for Batched Network Coding
   Jie Wang, Zhiyuan Jia, Hoover H. F. Yin, Shenghao Yang. 2021 IEEE International Symposium on Information Theory (ISIT)

7. Upper Bound Scalability on Achievable Rates of Batched Codes for Line Networks
   Shenghao Yang, Jie Wang. 2020 IEEE International Symposium on Information Theory (ISIT)

8. On the Capacity Scalability of Line Networks with Buffer Size Constraints
   Shenghao Yang, Jie Wang, Yanyan Dong, Yiheng Zhang. 2019 IEEE International Symposium on Information Theory (ISIT)

9. Finite-length Code and Application in Network Coding
   Shenghao Yang, Yanyan Dong, Jie Wang. IEEE INFORMATION THEORY SOCIETY GUANGZHOU CHAPTER NEWSLETTER, No.1, July 2020